下週(12/01)不用上課~
耶~
1124 作業
- 上全國碩博士論文,
- 找出哪些是關鍵字、哪些是動詞。
- 題目:應用數位學習平台探討國小學童科學批判思考與自我概念
- 關鍵字:數位學習平台、國小學童、科學批判思考、自我概念
- 動詞:應用、探討
- 並把題目改寫、重新排列組合。例如題目為:
- 「運用FB建構社區網絡社群粉絲團參與度研究」
關鍵字有:FB、網路社群、粉絲團、參與度- 原題目:應用數位學習平台探討國小學童科學批判思考與自我概念
- 改寫一:數位學習平台對於國小學童科學批判思考與自我概念之探討
- 改寫二:國小學童應用數位學習平台對科學批判思考與自我概念之探討
- 改寫三:探討國小學童應用數位學習平台對科學批判與自我概念之成長
- 「電腦支援合作學習對國小學童因數概念學習之研究」
關鍵字有:電腦支援、合作學習、因數概念、學習
這一篇的前言就可以寫:因數概念學習一直是~困擾之類的,接著舉出例子。
- 國小學童在科學批判思考的態度與學習,一直是令教師困擾的學習項目之一;要兼顧科學批判思考的角度進行學童的自我概念探討,更是被視為不可能的任務。故研究者認為,學童在校內進行的學習時間無法增加的前提之下,或許數位學習平台可以被視為是一種可行的探索方式。
- 「運用FB建構社區網絡社群粉絲團參與度研究」
- 找出哪些是關鍵字、哪些是動詞。
- http://www.pac.nctu.edu.tw/Homework/
余英時博士(國立交通大學名譽博士、中央研究院院士)
- 挑幾句話,作成簡單的心智圖
- 找出重點並摘要出來,請試著用這種方式寫出『心得感想』,重新詮釋挑出來的句子。
- 學者余英時在演講中說道:「分歧和衝突反而是文化最有生命力的表現。」以這句話來看我們個人乃至擴大到整個生存環境,無一不是衝突與分歧之下的產物。小至個人在腦海中激盪出來的創意、大至團體間創造出來的火花,這些都是經過一次次、一幕幕的衝突而誕生的。
- 上網找Jay Cross的東西
- 思維大師Jay Cross:變動世界的領導統御
- 定義「e-Learning」與「Workflow Learning」
- "Change direction. Think big. Work smarter. Hire Jay."
- 領域:
- cognitive science
- business administration
- how people learn
- social computing
- brain science
- psychology & motivation
1124 論文結構
題目(關鍵字寫出名詞)Title
第一章、前言 Introduction
第三章 研究設計 Research Design
第四章 研究發現 Research Finding/ Result
第五章 研究結論 Research Conclusion
第六章 參考文獻 Conference
- 把想要做的關鍵字找出來,拼拼湊湊就可以湊出三個論文題目,然後給老師選擇。
第一章、前言 Introduction
- 第一節 研究背景(大家公認很重要)
- 例如:「數位學習已經成為資訊社會的趨勢」通常後面要括弧備註引言人←破題。
- 第二節 研究動機(自己主觀性認為很重要)
- 通常使用三段論。
- 第三節 研究目的與問題
- 研究假設,是要假設相同還是假設不相同呢?這個研究假設,是研究者『針對研究問題』所提出的『可能的』答案。使用虛無假設,並推翻假設證明是有用的。
- 研究假定,是「排除不相關的變項」,亦即控制變項,例如:外面的聲響不會影響到實驗。
- 第四節 研究範圍與限制
- 研究限制,也就是『做不到』的。例如:本研究有以下的限制,研究時間只進行四週。本研究僅限於使用~量表。
- 第五節 重要名詞詮釋
名詞解釋有兩種撰寫方式:
- 自己系所的定義解釋(操作型定義)。
- 大家認定的定義解釋(概念型定義)。
第三章 研究設計 Research Design
第四章 研究發現 Research Finding/ Result
第五章 研究結論 Research Conclusion
第六章 參考文獻 Conference
1117 複習:中央極限定律、區間估計值
樣本平均數與母群平均數是有一個相關性的。
中央極限定律
中央極限定律
- 中央極限定律(The Central Limit Theorem)是一個非常有用的定律,因為它描述了平均數之樣本分配的特質。這個定律如下:
- 當母群存在著變異數和平均數時,如果樣本的樣本數夠大,則樣本平均數形成的機率分配(稱為平均數的樣本機率分配;sampling distributionof means)會趨近於常態分配;且當樣本數增大時,樣本機率分配會越趨近於常態分配。
- 搜尋的範圍越大,準確度越高
- 搜尋的範圍越小,準確度越低,實用性越高
1117 平均數考驗
1117 實做
課堂實做
態度量表,就像是期末教學量表一樣。
態度量表,就像是期末教學量表一樣。
- 請模擬態度量表有無改變,製作出一個30人的問卷量表,最低分1最高分5。
算出三次(甲乙丙班級)的前測成績。=RAND()*4+1 - 貼到SPSS內
- 敘述統計→描述性統計
- 比較平均數法→單因子變異數分析
(第二次)勾選「選項」→「描述性統計量」 - 比較平均法→獨立樣本T檢定
(第二次)點選「定義組別」→「輸入1、2」
- 獨立樣本檢定「t」的那一欄位其實是不需要的
- 雙尾(平均分配在兩側2.5%區域的)顯著性
- 單尾(偏某一側變成5%區域的)顯著性
- 準確率95% → 0.050 錯誤率,以 * 代替
- 準確率91% → 0.010 錯誤率,以 ** 代替
- 準確率100% → 0.000 錯誤率,以 *** 代替
1110 課堂實做
 |
| 圖示:已知樣本與已知母群標準差推估母群平均數 |
→範圍越小,區間估計值準確度越高
- 打開excel文件
- A1至A30寫輸入1,A31到A60輸入2,A61到A90輸入3
- 在B1到B90製作出範圍在30-60的亂數90組
- 選取複製、在C以及D內 貼上『值』,並注意儲存格式不能有小數點
- 將B刪除,複製A到C的所有數值
- 打開SPSS,將數值貼上
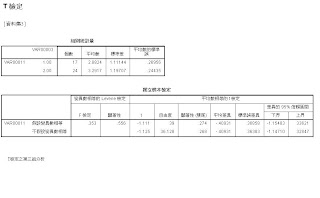
- 進行「單因子T檢定」分析
 |
| 圖示:T test |
 |
| 圖示:T test |
 |
| 圖示:T test |
- 步驟如上1到4
- 修改B的數值,改為取35到60的亂數90組
- 選取複製、在E內 貼上『值』,並注意儲存格式不能有小數點
- 將B刪除,複製A到D的所有數值
- 打開SPSS,將數值貼上
- 進行「單因子變異數」分析
 |
| 圖示:變異數 |
 |
| 圖示:變異數 |
 |
| 圖示:變異數 |
1110 小筆記:抽樣誤差
單一母數區間估計
↓
抽樣抽取一個樣本(平均數、標準差)
舉例:
十個數字1.2.3.4.5.6.7.8.9.1 進行抽樣
抽樣誤差 + 樣本平均數 = 母群平均數
舉例:
把母群畫數畫一條直線,取四次抽樣之後。
只是,到底要拉到多長,才能夠知道真正的母群平均數在哪?
舉例一:
+++課本的例子+++
假設一群男生內隨便抽十個量體重,樣本的數字為68.66.59.64.56.49.58.65.54.61。
平均數Medium為60
當樣本平均數為60。估計母群平均數為M = 60 +/- ? ←抽樣誤差
SD = 1.89 → m = 60 + ( SD x ? )
舉例二:
九個數字1.2.3.4.5.6.7.8.9 抽樣如下圖。
(數字一抽到一次,二抽到兩次~)
M=5時
抽出來的樣本假設是7,這個7代表是真正的母群數加上抽樣誤差(7 = 5 + 抽樣誤差)。
舉例三:
射飛鏢,以射的點為中心畫半徑1.5公分內(95% 的抽樣誤差)一定會有紅心存在。
↓
抽樣抽取一個樣本(平均數、標準差)
舉例:
十個數字1.2.3.4.5.6.7.8.9.1 進行抽樣
→會發現抽出來的值有一個特質,也就是在範圍2.5到8.5之間。
抽樣誤差 + 樣本平均數 = 母群平均數
舉例:
把母群畫數畫一條直線,取四次抽樣之後。
→當把樣本平均數展開一個範圍時,會發現這個範圍會包含真正的母群平均數。
只是,到底要拉到多長,才能夠知道真正的母群平均數在哪?
舉例一:
+++課本的例子+++
假設一群男生內隨便抽十個量體重,樣本的數字為68.66.59.64.56.49.58.65.54.61。
平均數Medium為60
當樣本平均數為60。估計母群平均數為M = 60 +/- ? ←抽樣誤差
SD = 1.89 → m = 60 + ( SD x ? )
舉例二:
九個數字1.2.3.4.5.6.7.8.9 抽樣如下圖。
(數字一抽到一次,二抽到兩次~)
M=5時
抽出來的樣本假設是7,這個7代表是真正的母群數加上抽樣誤差(7 = 5 + 抽樣誤差)。
舉例三:
射飛鏢,以射的點為中心畫半徑1.5公分內(95% 的抽樣誤差)一定會有紅心存在。
1110 小筆記:虛無假設
虛無假設 Null Hypothesis
關於某母體參數的敘述,通常是表示『沒有差異』的假設,又稱為「原假設」。
在奈曼—皮爾生的架構裡,有一虛無假設 null hypothesis 及一對立假設 alternative hypothesis。虛無假設通常表示現況,而對立假設表示我們傾向相信的,也就是想證明它是真者。
在假設檢定的過程中,所能忍受的錯誤機率有多大,則要視情況而定。以誤判的機率而言,事實上這中間有兩種錯誤的機率,其一是虛無假設為真卻拒絕(這稱為第一型錯誤),其二是虛無假設不真卻接受(這稱為第二型錯誤)。理想的狀況當然是兩型錯誤機率皆為 0,但通常不會有這種情形。當樣本數固定時,一般而言,兩型錯誤的機率,有一減小另一必增大。
由於虛無假設是真卻誤判它不真的後果往往較嚴重,所以通常的作法是先控制第一型錯誤的機率不要超過某一事先設定的值,然後使第二型錯誤的機率愈小愈好。
資料來源
雄大學應數系 黃文璋
銘傳大學網路服務處
關於某母體參數的敘述,通常是表示『沒有差異』的假設,又稱為「原假設」。
在奈曼—皮爾生的架構裡,有一虛無假設 null hypothesis 及一對立假設 alternative hypothesis。虛無假設通常表示現況,而對立假設表示我們傾向相信的,也就是想證明它是真者。
在假設檢定的過程中,所能忍受的錯誤機率有多大,則要視情況而定。以誤判的機率而言,事實上這中間有兩種錯誤的機率,其一是虛無假設為真卻拒絕(這稱為第一型錯誤),其二是虛無假設不真卻接受(這稱為第二型錯誤)。理想的狀況當然是兩型錯誤機率皆為 0,但通常不會有這種情形。當樣本數固定時,一般而言,兩型錯誤的機率,有一減小另一必增大。
由於虛無假設是真卻誤判它不真的後果往往較嚴重,所以通常的作法是先控制第一型錯誤的機率不要超過某一事先設定的值,然後使第二型錯誤的機率愈小愈好。
資料來源
雄大學應數系 黃文璋
銘傳大學網路服務處
1110 小筆記:T檢驗
什麼是T檢驗
T檢驗,亦稱 s t udent T檢驗(Student's T test),主要用於樣本含量較小(例如n<30),總體標準差σ未知的正態分佈資料。
T檢驗是用於小樣本(樣本容量小於30)的兩個平均值差異程度的檢驗方法。它是用T分佈理論來推斷差異發生的概率,從而判定兩個平均數的差異是否顯著。
T檢驗是戈斯特為了觀測釀酒質量而發明的。戈斯特在位於都柏林的健力士釀酒廠擔任統計學家,基於Claude Guinness聘用從牛津大學和劍橋大學出來的最好的畢業生以將生物化學及統計學應用到健力士工業程式的創新政策。戈特特於1908年在Biometrika上公佈T檢驗,但因其老闆認為其為商業機密而被迫使用筆名(學生)。實際上,戈斯特的真實身份不只是其它統計學家不知道,連其老闆也不知道。
單個樣本的t檢驗
目的:比較樣本均數所代表的未知總體均數μ和已知總體均數μ。
配對樣本t檢驗
目的:判斷不同的處理是否有差別 。
T 分配表
當n小於30,要用t分配去看而非看常態分配。
舉例:
樣本 = 60
標準差SD = 1.89
-----> 平均數m = 60 + ( SD x ? )
-----> 60 + 1.89 x 2.262 95% 準確時套用0.025
-----> 60 + 1.89 x 3.25 99% 準確時套用0.005
自由度
二點成一平面,自由度為1(2-1)
三點成一平面,自由度為2(3-2)
樣本是14就看t分配13那一欄位。
雙側考驗:有正有負的
單側考驗:一定是大於某數的
資料來源
T檢驗,亦稱 s t udent T檢驗(Student's T test),主要用於樣本含量較小(例如n<30),總體標準差σ未知的正態分佈資料。
T檢驗是用於小樣本(樣本容量小於30)的兩個平均值差異程度的檢驗方法。它是用T分佈理論來推斷差異發生的概率,從而判定兩個平均數的差異是否顯著。
T檢驗是戈斯特為了觀測釀酒質量而發明的。戈斯特在位於都柏林的健力士釀酒廠擔任統計學家,基於Claude Guinness聘用從牛津大學和劍橋大學出來的最好的畢業生以將生物化學及統計學應用到健力士工業程式的創新政策。戈特特於1908年在Biometrika上公佈T檢驗,但因其老闆認為其為商業機密而被迫使用筆名(學生)。實際上,戈斯特的真實身份不只是其它統計學家不知道,連其老闆也不知道。
單個樣本的t檢驗
目的:比較樣本均數所代表的未知總體均數μ和已知總體均數μ。
配對樣本t檢驗
目的:判斷不同的處理是否有差別 。
T 分配表
當n小於30,要用t分配去看而非看常態分配。
 |
| 圖示:T 分配表 |
樣本 = 60
標準差SD = 1.89
-----> 平均數m = 60 + ( SD x ? )
-----> 60 + 1.89 x 2.262 95% 準確時套用0.025
-----> 60 + 1.89 x 3.25 99% 準確時套用0.005
自由度
二點成一平面,自由度為1(2-1)
三點成一平面,自由度為2(3-2)
樣本是14就看t分配13那一欄位。
雙側考驗:有正有負的
單側考驗:一定是大於某數的
資料來源
1103 課堂作業
課堂實做:
心得:
我們這一組算出的平均根本就不準哪!
應該是要十抽七會比十抽四平均的吧,結果平均之後發現我們的十抽四還比較接近平均數 orz
- 十抽七,算出每一次的平均,最後加總再平均
- 十抽四,算出每一次的平均,最後加總再平均
心得:
我們這一組算出的平均根本就不準哪!
應該是要十抽七會比十抽四平均的吧,結果平均之後發現我們的十抽四還比較接近平均數 orz
1103 小筆記:常態累積機率表、SPSS 區間估計
常態累積機率表
+/-誤差3%,百分點在0.9750
使用SPSS製作『常態累積機率』檢驗 單因子變異數分析
→輸入三十個數字兩行
→把兩行都圈選起來
→選擇分析
→選擇比較平均數法
→選擇單一樣本T檢定
→選擇兩行數字
→按下確定
差異的95%信賴區間的『上下界』是什麼意思:
範本平均數在這兩個值(上界x1.96、下界x0.3)之間
+/-誤差3%,百分點在0.9750
使用SPSS製作『常態累積機率』檢驗 單因子變異數分析
→輸入三十個數字兩行
→把兩行都圈選起來
→選擇分析
→選擇比較平均數法
→選擇單一樣本T檢定
→選擇兩行數字
→按下確定
差異的95%信賴區間的『上下界』是什麼意思:
範本平均數在這兩個值(上界x1.96、下界x0.3)之間
1103 小筆記:誤差、類型錯誤
母群
1.2.3.4.5.6.7.8.9.10
取五個樣本
當取樣的次數越多時,平均會越接近五。
十抽十,抽樣誤差為+/- 0,樣本數與準確度並不是成正比的,但可以確定的是,抽越少成本越低但是越不準。不過以台灣而言,無論母群多大,樣本數超過300就已經算多了。
根據常態分班,全班的智力(訂為A)測驗總平均為100(實線)。
假設讓全校(訂為B)的學生做智力測驗,總平均是103(虛線)。
從A到B稱為『偏移』,又假設在這個偏移之中出現了102?
這個102到底是A圖的曲線還是B圖的?要怎麼分辨呢?
所以這個時候就會需要用套『推論統計』,必須用到『假設→事實』的九宮格。
1.2.3.4.5.6.7.8.9.10
取五個樣本
 |
| 圖示:取樣 n 數 |
十抽十,抽樣誤差為+/- 0,樣本數與準確度並不是成正比的,但可以確定的是,抽越少成本越低但是越不準。不過以台灣而言,無論母群多大,樣本數超過300就已經算多了。
根據常態分班,全班的智力(訂為A)測驗總平均為100(實線)。
假設讓全校(訂為B)的學生做智力測驗,總平均是103(虛線)。
從A到B稱為『偏移』,又假設在這個偏移之中出現了102?
這個102到底是A圖的曲線還是B圖的?要怎麼分辨呢?
所以這個時候就會需要用套『推論統計』,必須用到『假設→事實』的九宮格。
 |
| 圖示:上課教材- type 2 |
分享:無罪推定原則與富士康,張瑞雄。2010/06/23 蘋果日報
純粹覺得這個詞好熟悉呀!
『無罪推定』的觀念應用於社會事件上,跟大家分享一下,呵呵~
全文轉自:http://www.coolloud.org.tw/node/52858
最近幾位學者和大學教授批評郭台銘大陸的富士康公司是血汗工廠,郭台銘是台灣之恥。但行政院長予以緩頰,認為批評太超過。現代民主國家法律的一個重要的基石是無罪推定原則,我國《刑事訴訟法》第154條明文:「被告未經審判證明有罪確定前,推定其為無罪。犯罪事實應依證據認定之,無證據不得認定犯罪事實。」無罪推定原則是國際公約確認和保護基本人權,也是聯合國在刑事司法領域制定和推行的最低限度之一。
但是這種「除非證明有罪,否則無辜」的普世原則,在台灣卻變成「除非證明無辜,否則有罪」。這種現象即使在講求嚴謹的學術理論和證據的學術界也無法倖免,例如在此富士康事件中,學者們沒有到富士康公司實際調查過,但是套用學者的話,「郭台銘如果認為自己的富士康工廠運作符合國際勞動人權,就應該開放讓學者前往進行勞動調查。」這也就是典型的「除非證明無辜,否則有罪」。
本來是控方要努力找證據來證明你有罪,現在變成你自己要拚命找證據來證明你的清白,這種現象讓「戴帽子」很容易,例如「紅帽子」一戴,你就要撇清與中國的關係,否則就是賣台。「除非證明無辜,否則有罪」的心態讓台灣變成一個不信任的社會,兩黨互不信任,政府和百姓也互不相信,到最後甚至變成「被判無罪以後,還是不表示沒犯罪,可能是運氣好」,這絕非國家和人民之福。
有幾分證據講幾分話
幾年前一位衛生署長的烏龍舔耳案鬧得沸沸揚揚,在政治人物和媒體的推波助瀾下,當時民調有高達百分之八十幾的受訪者相信署長是有責的,最後雖然證明清白,但傷害已經造成,無法彌補。故在一個民主成熟而崇尚法治的社會,在事理未明之前,媒體對於公眾人物的違法失職嫌疑,在被證明有罪之前,如何拿捏揭弊和無罪推定之間的分寸,是社會大眾和媒體需要智慧的地方。
如何讓台灣民眾堅守無罪推定的原則,如何不再理盲,如何不再沒證據而起鬨?可能沒有完美或單一的答案,但至少可以從學校開始,從老師信任學生,學者有幾分證據講幾分話做起。
『無罪推定』的觀念應用於社會事件上,跟大家分享一下,呵呵~
全文轉自:http://www.coolloud.org.tw/node/52858
最近幾位學者和大學教授批評郭台銘大陸的富士康公司是血汗工廠,郭台銘是台灣之恥。但行政院長予以緩頰,認為批評太超過。現代民主國家法律的一個重要的基石是無罪推定原則,我國《刑事訴訟法》第154條明文:「被告未經審判證明有罪確定前,推定其為無罪。犯罪事實應依證據認定之,無證據不得認定犯罪事實。」無罪推定原則是國際公約確認和保護基本人權,也是聯合國在刑事司法領域制定和推行的最低限度之一。
但是這種「除非證明有罪,否則無辜」的普世原則,在台灣卻變成「除非證明無辜,否則有罪」。這種現象即使在講求嚴謹的學術理論和證據的學術界也無法倖免,例如在此富士康事件中,學者們沒有到富士康公司實際調查過,但是套用學者的話,「郭台銘如果認為自己的富士康工廠運作符合國際勞動人權,就應該開放讓學者前往進行勞動調查。」這也就是典型的「除非證明無辜,否則有罪」。
本來是控方要努力找證據來證明你有罪,現在變成你自己要拚命找證據來證明你的清白,這種現象讓「戴帽子」很容易,例如「紅帽子」一戴,你就要撇清與中國的關係,否則就是賣台。「除非證明無辜,否則有罪」的心態讓台灣變成一個不信任的社會,兩黨互不信任,政府和百姓也互不相信,到最後甚至變成「被判無罪以後,還是不表示沒犯罪,可能是運氣好」,這絕非國家和人民之福。
有幾分證據講幾分話
幾年前一位衛生署長的烏龍舔耳案鬧得沸沸揚揚,在政治人物和媒體的推波助瀾下,當時民調有高達百分之八十幾的受訪者相信署長是有責的,最後雖然證明清白,但傷害已經造成,無法彌補。故在一個民主成熟而崇尚法治的社會,在事理未明之前,媒體對於公眾人物的違法失職嫌疑,在被證明有罪之前,如何拿捏揭弊和無罪推定之間的分寸,是社會大眾和媒體需要智慧的地方。
如何讓台灣民眾堅守無罪推定的原則,如何不再理盲,如何不再沒證據而起鬨?可能沒有完美或單一的答案,但至少可以從學校開始,從老師信任學生,學者有幾分證據講幾分話做起。
1027 小筆記:中央極限定理
A 母群只有一個(台北縣的人口)
B 樣本(甲乙兩公司的抽樣)
→但 A B 公司的樣本數推論回母群會有不一樣的結果。
上述現象即為中央極限定理
十個抽十個最準確,十個抽五個準確機率只有一半。
十個抽五個,總算三次統計,再把三次統計加起來平均,會更準確。
例如:10.9.8.7.6.5.4.3.2.1的平均數是5.5
第一次 10.8/2 = 9
第二次 7.3/2=5
第三次 10.2/2=6
9.5.6/3=6.666 ← 這個數字會更趨近於平均數
B 樣本(甲乙兩公司的抽樣)
→但 A B 公司的樣本數推論回母群會有不一樣的結果。
上述現象即為中央極限定理
十個抽十個最準確,十個抽五個準確機率只有一半。
十個抽五個,總算三次統計,再把三次統計加起來平均,會更準確。
例如:10.9.8.7.6.5.4.3.2.1的平均數是5.5
第一次 10.8/2 = 9
第二次 7.3/2=5
第三次 10.2/2=6
9.5.6/3=6.666 ← 這個數字會更趨近於平均數
1027 小筆記:假設與判斷
 |
| 圖示:判斷的方法 |
問題→某甲是否偷竊?
假設→無罪推論:某甲沒有偷竊。有罪推論:某甲有偷竊。
 |
| 圖示:判斷四種假設 |
 | |
| 圖示:四種假設的判斷結果 |
但是裡面會有錯誤機率:也就是「有些機率是可以被容許的」。
第一類型錯誤 type 1 error = α 最嚴重的
第二類型錯誤 type 2 error = β