- 平常不去進行現象觀察的時候，就會找不到研究問題，若沒有研究問題，就沒有研究假設，當沒有研究假設，就沒有研究可以做，那就畢不了業哩～
例如：假設用某某方法有用，則必須去證明，這個證明的過程，就是一個論文的產生。
- 要素範圍：數位學習科技
現象：應用在某學生上、某教材、某課程上有用嗎？
假設效用：可能的結果為何？
- 統計學應用問卷：教學歷程、學習歷程
問卷內容：認知心理學
出題：行為模式
- 最好先用心智圖先把第一層架構找出來
1027 小筆記：應用與提醒
1027 小筆記：推論統計 - 機率
「從實招來，
有罪推論（從犯罪事實去搜查證據（反向推論）依照過去的行為來判斷），
無罪推論」
「多做實驗性的研究（有無效果）、多做統計的研究。」
「大膽假設，小心求證。」
問題problem / question：很難清楚的去找到真相的。
研究假設hypothesis：
有罪推論（從犯罪事實去搜查證據（反向推論）依照過去的行為來判斷），
無罪推論」
「多做實驗性的研究（有無效果）、多做統計的研究。」
「大膽假設，小心求證。」
問題problem / question：很難清楚的去找到真相的。
研究假設hypothesis：
- 針對研究問題，研究者認為可能的答案。
- 從現象問題延伸出來的問題。
- 會根據事實來做判斷，當事實無法做判斷時，會憑藉著發生錯誤的機率有多少來避開，發生錯誤的機率內有比較嚴重的錯誤叫做type1error 沒有的說有 type2error有的說沒有。
1020 作業：找出十句對自己有啟發的句子
- 恭喜你對人類的知識有所創新，因此授予你這個學位。
- 所有的精力、所有修課以及讀的書裡面都應該要有一個關注的焦點。
- 自己本身必須是帶著問題來探究無限的學問世界。
- 努力讓自己的學習產生自發的延展性是很重要的。
- 挑戰一個你做不到的東西。
- 清楚知道從哪裡開始，也要知道從哪裡放手。
- 要建構一個屬於自己的知識樹。
- 那重要的五、六本書要讀好幾遍。精讀原典。
- 尋找一個有意義、有延展性、可控制、可以經營的問題，而且不要太難。
- 留下時間，精緻思考。
1020 家庭小作業
- 使用Free Mind製作三個心智圖：
→汽車、新竹教育大學、最後一個自訂
- 結構→知識結構→上網找一篇王汎森院士（中央研究院歷史語言研究所）的《如果讓我重做一次研究生》，因為本篇文章具有結構性，請試著將文章的主要論點摘要起來。（讀全文、摘要）
- 找出《如果讓我重做一次研究生》文章內，十句對自己有啟發的句子
1020 非常態分配之曲線
非常態分配：
A’以及A是同等面積的，尾巴往右是正偏態，尾巴往左是負偏態。
正：當人當很多課的是正偏態。
負：美術等勞作課程是負偏態。
常態：
中數眾數平均數都落在同一點上面。平均數=中數=眾數
非常態（偏態）：
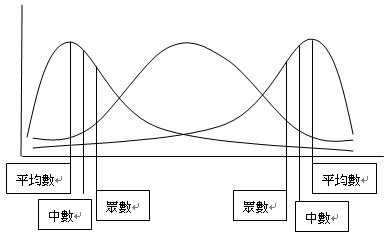
正偏態→平均數、眾數、中數往左邊移動。移動快慢：平均數>中數>眾數
負偏態→平均數、眾數、中數往右邊移動。移動快慢：眾數>中數>平均數
A’以及A是同等面積的，尾巴往右是正偏態，尾巴往左是負偏態。
正：當人當很多課的是正偏態。
負：美術等勞作課程是負偏態。
 |
| 圖示：非常態分配之常態化 |
常態：
中數眾數平均數都落在同一點上面。平均數=中數=眾數
非常態（偏態）：
正偏態→平均數、眾數、中數往左邊移動。移動快慢：平均數>中數>眾數
負偏態→平均數、眾數、中數往右邊移動。移動快慢：眾數>中數>平均數
 |
| 圖示：正負偏態 |
1020 數據解釋方式及運用
看常態曲線時，會有兩種解釋方式：
估計值：
假設一個班級第一次考試的分數是八十分，那第二次考試的平均八十分的機率多少？八十二分的機率又是多少？
百分等級：
典型標準分數是用人數來看的。（上週關鍵字）
魏氏量表：
一個標準差是15，兩個標準差是130，
- 數量的角度：有1000個人，有682個人在+/-1標準差之內。
- 機率的角度：用機率的角度，會有682次在+/-1標準差之內。
估計值：
假設一個班級第一次考試的分數是八十分，那第二次考試的平均八十分的機率多少？八十二分的機率又是多少？
百分等級：
典型標準分數是用人數來看的。（上週關鍵字）
魏氏量表：
一個標準差是15，兩個標準差是130，
1013 關鍵字
魏氏量表 WISC：是學校﹑特教機構﹑輔導機構以及醫院等單位經常使用的個別智力測驗。取自：阿元之家。
PR值 Percentile Rank：代表「位於某一原始分數以下的人數百分比」，亦即某一原始分數在團體每百人中分數所高過的人數。來自：國立臺中圖書館、104評量中心。
T分數 T-Score：T分數是由Z分數以線性轉換而得的標準分數。
- 本量表旨在測量受試者的普通能力。
- 全量表共有十二個分測驗，包括語文量表部份的五個分測驗：1.常識測驗2.類同測驗3.算術測驗4.詞彙測驗5.理解測驗和一個交替測驗 6.記憶廣度測驗；作業量表部份的五個分測驗為: 7.圖形補充測驗，8.連環圖系測驗，9.圖形設計測驗， 10.物形配置測驗， 11.符號替代測驗，和一個交替測驗為12.迷津測驗。
本量表採積點記分法，各分測驗的原始分數，可按年齡組別換算成單位相等的量表分數，各分測驗的分數相加，可得語文量表分數、作業量表分數和全量表總分，再 - 查對照表而得離差智商（M=100 ，SD=15）。
 |
| 圖示：魏氏量表百分比及分類 |
PR值 Percentile Rank：代表「位於某一原始分數以下的人數百分比」，亦即某一原始分數在團體每百人中分數所高過的人數。來自：國立臺中圖書館、104評量中心。
- 是先將該次測驗所有考生的5科總分排序後，依照人數均分成100等分，該生大約會落在第幾個等分中。
- 國中基測各科量尺分數為1至60分，分數愈高，代表該科能力愈好。
- 每一科的量尺分數是依所有考生答對題數的次數分配。
- 因具有和群體比較意義，像是用來測「量」個人表現的「尺」，稱為「量尺分數」。
 |
| 圖示：原始分數轉為 Z 分數的公式 |
 |
| 圖示：原始分數轉為 Z 分數公式～中文化 |
T分數 T-Score：T分數是由Z分數以線性轉換而得的標準分數。
- 公式為：Z分數 乘以 10 再加上 50
- T=50等於Z=0
1013 筆記
有兩個指標看這一群數字，一個是變異數，一個是平均數。
幅度越寬的，標準差就越大，則分散程度就越大。
Z分數 = 原來分數 – 平均分數 / 標準差
= 1.5 or 2.6 or 2.3 這個數字可以告訴你你離平均數有多遠
用標準差跟平均數來看這個分數在整體的定位，與另一個族群中的另一個數進行比較。
例如：甲班跟乙班比較，此為相對量數（標準分數）。
---下為課堂舉例---
成績的中數、平均數約273分
標準差內有二十萬人在內255492-49402=20690
幅度越寬的，標準差就越大，則分散程度就越大。
 |
| 圖示：變異數與平均數 |
Z分數 = 原來分數 – 平均分數 / 標準差
= 1.5 or 2.6 or 2.3 這個數字可以告訴你你離平均數有多遠
→和標準差差不多，大部分的學校是用T分數分發。
- Z分數：可發現相對高/低
→最多到3或4而已，剩下的1%是落到6以外（就叫做例外）。 - T分數：把Z分數x10 +50
→T=50等於Z=0
用標準差跟平均數來看這個分數在整體的定位，與另一個族群中的另一個數進行比較。
例如：甲班跟乙班比較，此為相對量數（標準分數）。
---下為課堂舉例---
成績的中數、平均數約273分
標準差內有二十萬人在內255492-49402=20690
 |
| 舉例：BCtest數據 |
 |
| 圖示：實際數據轉化為圖形 |
1006 關鍵字
T檢驗（t檢定）T-Test：使用平均數的概念。用於小樣本（樣本容量小於30）的兩個平均值差異程度的檢驗方法。它是用T分佈理論來推斷差異發生的概率，從而判定兩個平均數的差異是否顯著。
單因子變異數分析 One-way ANOVA：使用變異數的概念，ANOVA 是Analysis Of Variances的縮寫，是由R. A. Fisher所提出的統計方法，可解決同時檢定兩個或兩個以上樣本平均數的顯著性。
常態分配 normal distribution：指一個隨機變項的觀察值，呈現對稱的鐘形曲線分配，由德國數學家Gauss（Karl F. Gauss；1777-1855）所提出，因此又稱為高斯分配（Gaussian distribution）。統計上的常態分配（normal distribution）強調，在正常狀態下的個體一些屬性，包括身高、體重、智力……在數量的分布上皆呈現出兩極端占少數、中間部分占多數的分布情形。
六個標準差 Six Sigma：簡寫 為6σ。意即實際上消除企業在每一項產品、製程、以及互動方面的誤差，以接近其品質目標標準之品質頂尖水準程度，並減少「不良品質成本」（Cost of Poor Quality）、縮短交期（Cycle Time Reduction）、增進顧客滿意度的管理過程和企業衡量。Six Sigma是一種追求「最小變異」的經營管理思維，借用統計學上的常態分配與機率模式，來主導企業的戰略與戰術，此之經營理念在強力且有效的管理工具的配 合之下，大可從公司營運策略、管理方式一路做到產品研發、製程改善(作業改善)、品質提升、到售後服務滿意度的提升。五個階段：DMAIC——界定、衡量、分析、改善和控制
單因子變異數分析 One-way ANOVA：使用變異數的概念，ANOVA 是Analysis Of Variances的縮寫，是由R. A. Fisher所提出的統計方法，可解決同時檢定兩個或兩個以上樣本平均數的顯著性。
常態分配 normal distribution：指一個隨機變項的觀察值，呈現對稱的鐘形曲線分配，由德國數學家Gauss（Karl F. Gauss；1777-1855）所提出，因此又稱為高斯分配（Gaussian distribution）。統計上的常態分配（normal distribution）強調，在正常狀態下的個體一些屬性，包括身高、體重、智力……在數量的分布上皆呈現出兩極端占少數、中間部分占多數的分布情形。
六個標準差 Six Sigma：簡寫 為6σ。意即實際上消除企業在每一項產品、製程、以及互動方面的誤差，以接近其品質目標標準之品質頂尖水準程度，並減少「不良品質成本」（Cost of Poor Quality）、縮短交期（Cycle Time Reduction）、增進顧客滿意度的管理過程和企業衡量。Six Sigma是一種追求「最小變異」的經營管理思維，借用統計學上的常態分配與機率模式，來主導企業的戰略與戰術，此之經營理念在強力且有效的管理工具的配 合之下，大可從公司營運策略、管理方式一路做到產品研發、製程改善(作業改善)、品質提升、到售後服務滿意度的提升。五個階段：DMAIC——界定、衡量、分析、改善和控制
1006 作業：尋找標準差
（一）練習在excel內找標準差：
=STDEV()
=STDEVA()
（二）尋找工具
心智圖 Mind Map（Free Mind 有中文版）：作為研究工具裡面一個分類、腦力激盪很有效的一種工具。
相關網頁：
FreeMind 心智圖 Mindmap 教學 - 王永銘老師
XMind/FreeMind-心智圖的妙用 - 國立台灣大學，計算機及資訊網路中心
圖像學習 - 部落格《圖像學習（改善學習方法）》
跟心智圖類似的概念圖，是之前我自己找到的，加減跟大家分享一下嚕～
用概念圖理解論述架構 - 部落格《哲學哲學雞蛋糕》
=STDEV()
=STDEVA()
 |
| 上圖：SD 與Mean |
（二）尋找工具
心智圖 Mind Map（Free Mind 有中文版）：作為研究工具裡面一個分類、腦力激盪很有效的一種工具。
相關網頁：
FreeMind 心智圖 Mindmap 教學 - 王永銘老師
XMind/FreeMind-心智圖的妙用 - 國立台灣大學，計算機及資訊網路中心
圖像學習 - 部落格《圖像學習（改善學習方法）》
跟心智圖類似的概念圖，是之前我自己找到的，加減跟大家分享一下嚕～
用概念圖理解論述架構 - 部落格《哲學哲學雞蛋糕》
1006 筆記：標準差 stander deviation
簡稱SD，是一個母群體的概念。
SD 是一個非常有用的指標，MEAN 只是告訴你一個結果，無法像SD 可以判別狀態（分散或集中）。
母群 population（人口）：母群是浮動的。母群或許為（N已知and固定）or（N未知and不固定）通常在母群內找抽樣sampling（取樣），取出來的叫做Sample（樣本），以樣本進行計算，描述這個計算的結果，就叫做敘述統計。
一般來說，母群與樣本，是等比的增加或減少，而非固定。
調查：如果是取樣一千人，則這一千個樣本數，代表著總數約一千到一千五百萬的母群。
老師提醒：最少的樣本量是30，低於30，則樣本數不足，不足以取信於人。樣本數大於30，則會趨近於母群。
SD 是一個非常有用的指標，MEAN 只是告訴你一個結果，無法像SD 可以判別狀態（分散或集中）。
母群 population（人口）：母群是浮動的。母群或許為（N已知and固定）or（N未知and不固定）通常在母群內找抽樣sampling（取樣），取出來的叫做Sample（樣本），以樣本進行計算，描述這個計算的結果，就叫做敘述統計。
 |
| 上圖：推論 與 敘述 之差別 |
一般來說，母群與樣本，是等比的增加或減少，而非固定。
調查：如果是取樣一千人，則這一千個樣本數，代表著總數約一千到一千五百萬的母群。
老師提醒：最少的樣本量是30，低於30，則樣本數不足，不足以取信於人。樣本數大於30，則會趨近於母群。
 |
| 上圖：標準差計算概念 |
1006 筆記：平均數與變異量數差別
上週提到集中量數：平均數、中數、眾數、算術平均數。
變異量數 Measure of Variation 和集中量數 Measure of central location是一體兩面的。
→平均數 Mean 與標準差 Stand Deviation 是敘述統計裡面很重要的指標。
- 所代表的意義是集中趨勢
- 所有的數加起來如果有正與負，加起來一定等於零。
- 可能不存在。
| | 平均數Mean | 標準差 Stand Deviation | 說明 |
| 甲班 | 80 | 2.5 | 成績分散程度或許為75-85 |
| 乙班 | 80 | 4 | 成績分散程度或許為72-88 |
變異量數 Measure of Variation 和集中量數 Measure of central location是一體兩面的。
→平均數 Mean 與標準差 Stand Deviation 是敘述統計裡面很重要的指標。
 |
| 上圖：集中與變異量數的差別 |
為什麼要學統計？
九零年代爆發“量化研究”潮，而研究的蒐集結果，產生了大量的數字資料。而人腦無法處理龐大的資料，所以出現了“統計”，也就是，統計是使用在『當數字資料很龐大的時候』。
資料可以用來詮釋連續性的現象。
資料也可以是具有代表性的，但是代表性的資料通常是不連續的現象。
------
搜尋了關鍵字，找到一篇作者對於統計的概念，我覺得蠻適合提醒自己『統計』對於研究的重要性。
「統計學是科學研究中重要的工具之一，其角色定位在如何蒐集資料及利用該組資料做一正確分析。其目的在於從解決問題中所獲得之珍貴資料，尋找可以支持做成決策之科學方法。」引用自 BJ的網路書房
另找到一篇《如何學好統計》，來自臺大教學發展中心「學習策略工作坊」
大家共勉之～
資料可以用來詮釋連續性的現象。
資料也可以是具有代表性的，但是代表性的資料通常是不連續的現象。
------
搜尋了關鍵字，找到一篇作者對於統計的概念，我覺得蠻適合提醒自己『統計』對於研究的重要性。
「統計學是科學研究中重要的工具之一，其角色定位在如何蒐集資料及利用該組資料做一正確分析。其目的在於從解決問題中所獲得之珍貴資料，尋找可以支持做成決策之科學方法。」引用自 BJ的網路書房
另找到一篇《如何學好統計》，來自臺大教學發展中心「學習策略工作坊」
大家共勉之～
0929 關鍵字
量化研究 quantitative research：間斷，取樣sampling出來的，無法描述。
常模 norm：一個具有代表性的樣本群組之分佈。
質化研究（質性研究）qualitative research：因為量化無法描述，所以出現了質性研究，可連續性的描述。老師舉牧師講道為例：牧師看到的是表象（量化）的樣子，但實際上卻是另外一種意思（質化）
平均數 mean：是集中量數內的一個代表數。
中數 median ：取中間的數值。
眾數 mode：數量最大的。出現頻率最高的。
集中量數 Measure of central location：
(1)可能存在→所有的數字，會朝代表數字集中。會用一條數線畫出圖以做代表。
(2)可能不存在→如果是看月平均，那就更有可能不會實際存在於某一天。
常模 norm：一個具有代表性的樣本群組之分佈。
質化研究（質性研究）qualitative research：因為量化無法描述，所以出現了質性研究，可連續性的描述。老師舉牧師講道為例：牧師看到的是表象（量化）的樣子，但實際上卻是另外一種意思（質化）
平均數 mean：是集中量數內的一個代表數。
中數 median ：取中間的數值。
眾數 mode：數量最大的。出現頻率最高的。
集中量數 Measure of central location：
(1)可能存在→所有的數字，會朝代表數字集中。會用一條數線畫出圖以做代表。
(2)可能不存在→如果是看月平均，那就更有可能不會實際存在於某一天。
0929 練習
<<練習用SPSS>>
1. 先使用excel在A格內製作40個亂數（最低60最高85）
2. 再將40個數字 ” 選擇性貼上（選值）" 到旁邊的B格
3. 將B表格的數字貼在SPSS軟體內
選擇分析→敘述統計→描述性統計量→點選”選項”（選擇自己要的項目）→the end
選擇分析→敘述統計→次數分配表→點選”選項”（選擇自己要的項目）→the end
─備註─
亂數=RAND()*A+B) ← 取A到B之間的數值
總和=SUN()
中數=MEDIAN()
算術平均數=AVERAGE()
眾數=MODE() 在excel內不是整數無法找出眾數，但SPSS可以……
990915 小筆記
1. 教材使用 林清山《教育統計學》加上SPSS資料統計軟體
2. 現場製作關鍵字文件，製作自己的知識結構筆記
3. 製作Blog，建立本課程的自我學習歷程（分數佔50%哪......）
(1) 呈現自我知識結構
(2) 呈現個人觀點
2. 現場製作關鍵字文件，製作自己的知識結構筆記
3. 製作Blog，建立本課程的自我學習歷程（分數佔50%哪......）
(1) 呈現自我知識結構
(2) 呈現個人觀點
可代表『聚集』的名詞
平均數 mean ：是集中量數內的一個代表數。
中數 median：取中間的數值。
眾數 mode：數量最大的。出現頻率最高的。
集中量數 mensure of central location：
(1)可能存在→所有的數字，會朝代表數字集中。會用一條數線畫出圖以做代表。
(2)可能不存在→如果是看月平均，那就更有可能不會實際存在於某一天的數字出現。
中數 median：取中間的數值。
眾數 mode：數量最大的。出現頻率最高的。
集中量數 mensure of central location：
(1)可能存在→所有的數字，會朝代表數字集中。會用一條數線畫出圖以做代表。
(2)可能不存在→如果是看月平均，那就更有可能不會實際存在於某一天的數字出現。
990915 公告
上課時間修正
因應老師的趕課時間與同學的肚子消化時間 XDDDD
1840 開始上課
1920 上課告一段落的試作（一）
2000 繼續上課
2030 上課告一段落的試作（二）
上課地點
推廣大樓3樓9307室
上課內容順序
研究統計 CH3 → 研究目的 CH1 → 文獻探討 CH2
工具軟體
1. SPSS
2. Weboffice : 140.126.36.92
聯絡資訊
王老師 dmwang@mail.nhcue.edu.tw
美萱學姐 madge29892@hotmail.com
因應老師的趕課時間與同學的肚子消化時間 XDDDD
1840 開始上課
1920 上課告一段落的試作（一）
2000 繼續上課
2030 上課告一段落的試作（二）
上課地點
推廣大樓3樓9307室
上課內容順序
研究統計 CH3 → 研究目的 CH1 → 文獻探討 CH2
工具軟體
1. SPSS
2. Weboffice : 140.126.36.92
聯絡資訊
王老師 dmwang@mail.nhcue.edu.tw
美萱學姐 madge29892@hotmail.com